Netlist and System Partitioning : KL 알고리즘

<오류의 지적을 매우 환영합니다.>

 

VLSI의 디자인이 복잡해짐에 따라, 설계에 있어 자동설계는 필수적인 기술이 되었다.

 

하지만 게이트의 수가 많아지고, 이들을 물리적으로 연결하는 Physical design 단계에서 복잡도가 크기에 비해 지수적으로 증가하자, 공학자들은 분할정복(Divide and Conquer) 방식을 이용하여 이를 해결하려 하였다.

 

이 방법은 말그래도 Gate-level-netlist를 서로 독립적인 여러 하위 회로로 분할하여, 따로 Place & Route를 진행하고, 이후 이를 다시 통합하여, Local Optimiztion을 만족시키는 것이다.

 

길게 설명을 했지만 한 줄로 요약하면, "회로를 쪼개서 각자 해결하고 합친다." 라고 생각하면 되겠다.

 

자 그러면 말그대로 그냥 막 자르면 되지 않나? 싶다면 아래 그림을 보자.

 

어떤 방향으로 자르는지에 따라 하위 회로끼리의 연결이 달라진다.

위 그림이 나타내는 것은, 우리가 자르는 방향에 따라 하위 회로끼리 연결해야 하는 갯수가 달라진다는 것이다.

(cut1 : 2개, cut2 : 4개)

 

우리가 회로를 쪼갠 이유가 무엇인가? 연산의 횟수를 줄이기 위함인건데, 하위 회로끼리 연결해야 하는 횟수가 많다면 굳이 회로를 쪼개서 처리를 한 이유가 없어진다.

 

따라서, 우리는 회로를 자르는 방법도 효율적으로 자르는 방법을 선택해야 할 필요성이 있어 여러 알고리즘을 사용하게 된다. (효율적인 것을 평가하는 지표로는 Edge가 잘리는 수와 하위 회로가 차지하는 면적 등이 있겠다.)

 

일단 알고리즘에서는 회로도를 사용하는 것이 아니라, 그래프로 표현된 자료를 처리하는 것이므로, 앞으로는 회로도를 그래프로 표현하도록 하겠다.

 

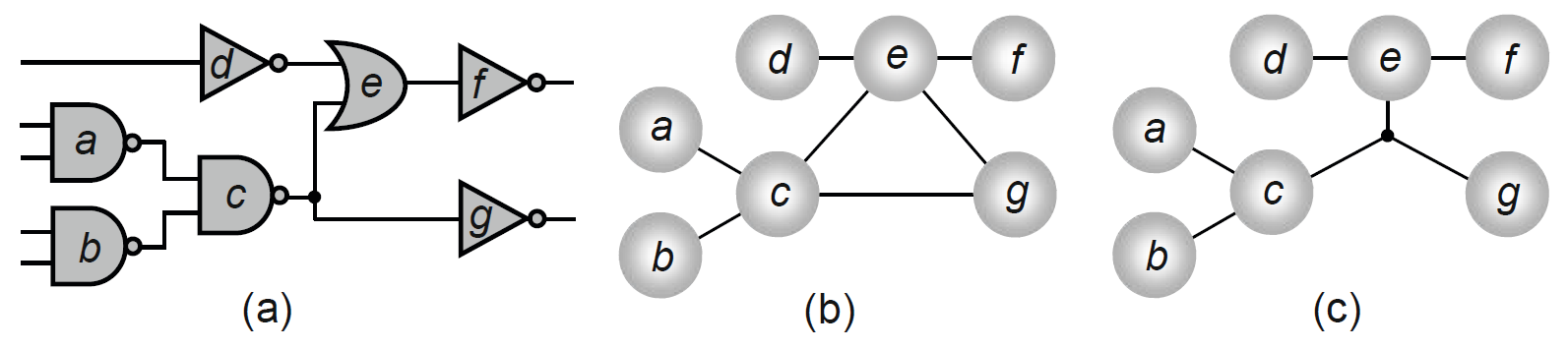
(a) 회로도 (b) 그래프 (c) 하이퍼그래프

 

Gate는 Node, 서로 간의 연결은 Edge로 표현하여 위 처럼 표현할 수 있다.

 

자 이제부터 본격적으로 CAD 분야에서 자주 사용되는 알고리즘인 Kernighan-Lin(KL)algorithm 에 대해서 다루려고 한다.

 

먼저 알고리즘의 pseudo code를 보도록 하자.

KL Algorithm의 pseudo code

처음 봤을 때, 솔직히 뭔 소린가 싶었다.

 

난 항상 예제를 통해 이해하는 것을 좋아해서 예제를 가져와 한 단계씩 확인해 보자.

 

1단계

 

위와 같은 그래프가 있다고 하자. 가운데 수평으로 나있는 긴 점선은 Cut Line을 의미하고, 그 위는 A회로(a, b, c, d), 그 밑은 B회로(e, f, g, h)라고 하자.

 

아무것도 하지 않고 이 상태로 회로를 자른다면, 9개의 Edge가 잘리게 되므로, cut cost는 9이다.

 

여기서 우리는 cut cost가 가장 작은 상태를 찾아야 하며, 이 알고리즘은 그 방법으로 Node의 자리를 서로 교환하는 방법을 선택했다. (A회로와 B회로끼리)

 

그러면 어떤 노드들을 서로 교환해야 가장 효율적인 상태를 유지할까?

 

여기서는 그걸 정량화하기 위해 D라는 Function을 정의하였다.

 

D(x) : x라는 노드를 반대편으로 넘겼을 때 얻는 Edge 이득

 

정도로 해석할 수 있겠다.

 

예를 들면 위 그림의 D(a)의 경우, a노드는 A회로에 있을 때 총 2개의 Edge가 잘린다.

 

그 상태에서 a노드를 B회로로 옮긴다면, 오로지 1개의 Edge만 잘린다.

 

따라서, a노드를 A에서 B로 옮겼을 때 얻는 Edge 이득은 1이 된다.

 

이런 식으로 모든 노드에 대해서 D 값을 도출하고, 두 노드를 Swap하였을 시 얻게 되는 총 이득 값(g)을 계산한다.

(여기서 c 값은 두 노드 사이의 Edge 연결 개수를 의미한다.)

 

2단계

위 그림과 같이 c와 e를 Swap한 뒤에는 c와 e를 바꾸어야 하는 노드의 집합에서 제거(Node fix)한다.

 

이후 같은 과정을 반복한다.

 

 

이렇게 모든 노드가 고정되었을 때(모든 노드를 한번씩 Swap하였을 때), 이전의 반복 과정에서 가장 좋았던 이득 값과 상태를 기억하여 되돌아 간다. 여기서는 반복 횟수 2번일 때, Gm이 8일 때이다.

 

따라서 이 알고리즘은 가장 Edge가 적게 잘리는 Path를 찾지는 못하지만, Greedy하게 Local Optimization을 찾을 수 있다.